Interactive Multi-View Stereo Simulator

Motivation

In the textbook scene with two rectified cameras (depicted below), using similar triangles $\triangle PC_1C_2 \sim \triangle C_2I_1I_2$, it follows that $\delta / f = B / D$, where $\delta$ is pixel disparity, $f$ is the focal length in pixels, $B$ is the camera baseline, and $D$ is depth to the observed world point.

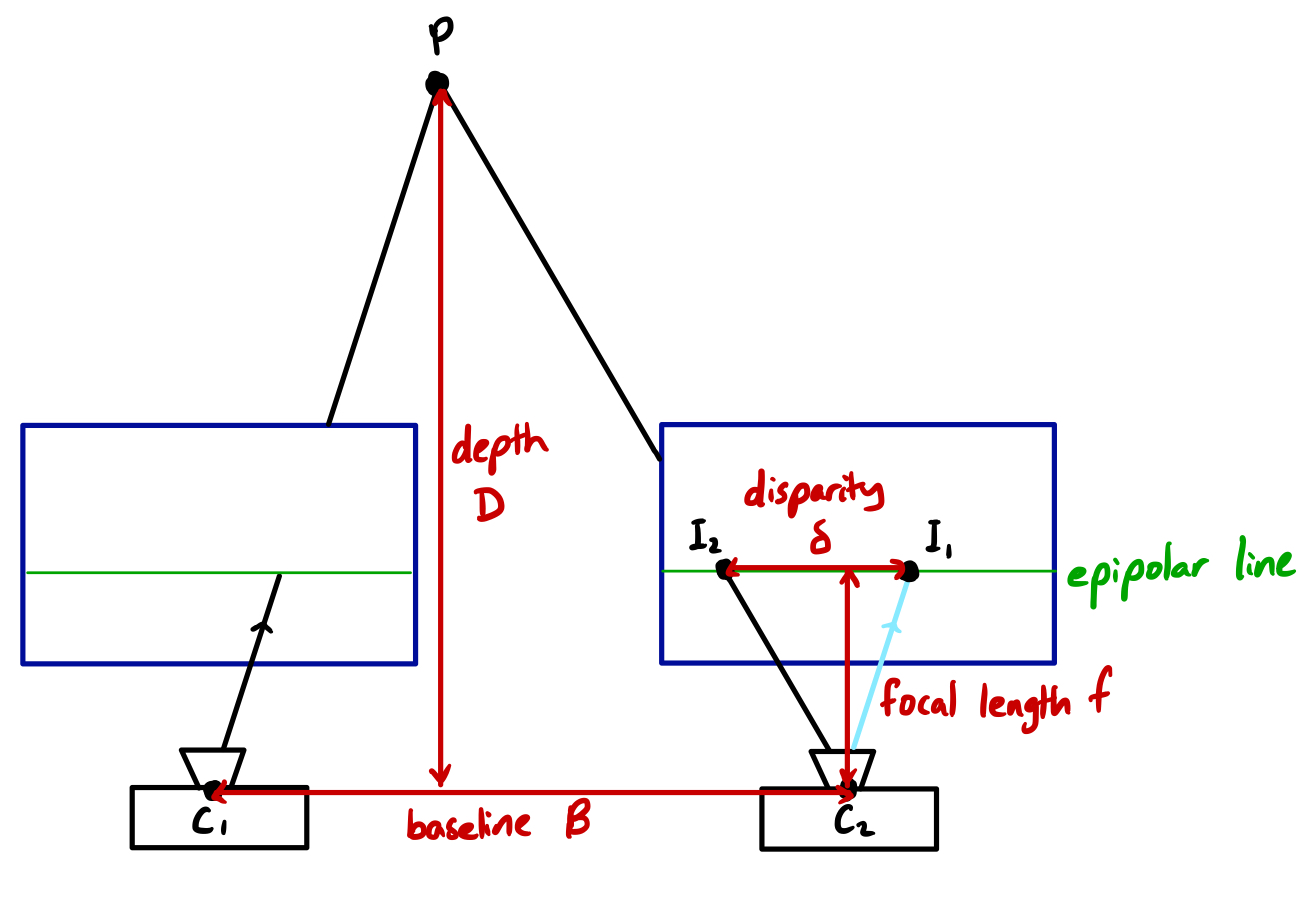
In this case, it’s simple to reason about how changes in camera parameters may affect the quality of the triangulation. Given a disparity measurement $\delta \pm \epsilon$ with $\epsilon$ pixels of uncertainty, we’re able to resolve depth to the range

\[\frac{B \cdot f}{\delta + \epsilon} \leq D \leq \frac{B \cdot f}{\delta - \epsilon}.\]

Now pin the depth of the observed point to $D$ and double the baseline $B$. The according disparity measurement will also double:

\[\frac{2B \cdot f}{2\delta + \epsilon} \leq D \leq \frac{2B \cdot f}{2\delta - \epsilon} \implies \frac{B \cdot f}{\delta + \epsilon / 2} \leq D \leq \frac{B \cdot f}{\delta - \epsilon / 2}.\]

That is, doubling the baseline $B$ has the same effect as halving the uncertainty $\epsilon$ in our disparity measurement.

Similarly, one can show that:

• doubling the focal length $f$ has the same effect as doubling the uncertainty $\epsilon$
• and doubling the depth $D$ of the observed point has the same effect as doubling the uncertainty $\epsilon$.

But what about for $N > 2$ cameras? How does reconstruction uncertainty scale with camera positions, orientations, and intrinsics? In the absence of nice closed form solutions for $N > 2$ cameras, can we simulate the observed uncertainty and observe how it responds? Gain some intuition or emulate your multi-view camera setup with the tool here!